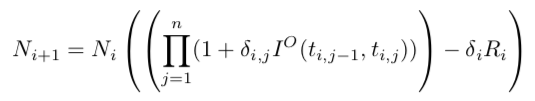Description
In this section we provide more details about the hybrid approach to the term sheet of bonds and loans. This is based on compounding in-arrears mechanism but with improvements that make them easier to deal with, specially in relation to the forecast of cashflows at the beginning of each period. This approach has been previously described in a December 2019 blog : Compounded rate out of favour: what now? (2).This type of approach may have been described before, but the author is not aware of any related literature.
At start of each period, a fixed rate is decided for the period. This rate is not a definitive rate, but an advance on interest rate. At the end of the period the standard compounded in-arrears rate is computed. The difference between the compounded rate and the advance is added to the notional to be repaid.
The way the rate fixed at the start of the period is not very important. Its impact on valuation or risk management is minor; it is of the same order of magnitude that a spread above compounded rate.
Set of payment related date: ti (i=0,..., n). t0 the start date and ti (i>0) the actual payment date. Each of the periods [ti-1,ti] (i=1,..., n) is divided in overnight periods (ti,j) (j=0,..., ni) with ti,0 = ti-1 and ti, ni = ti.
For a period notional Ni, the compounded interest amount is
The interest rate paid on the end of period i is Ri. The rate Ri is Fti-1-measurable, i.e. it is decided at (or before) the period start. After that period, the notional is adapted with
The total cashflow equivalent in ti is this the interest paid plus the notional increase. This is equal to
At the end of the last period, the amount repaid is notional plus interest, i.e.
Whatever the choice for Ri is done, in all cases, the periodic payment at each coupon date is equivalent to a compounded rate. The final payment include notional plus compounded interest. The notional is slightly change at each period but that does not bring any complexity as the rate is the fair rate for the period. It is not more complex than a loan/bond with variable notional paying floating fair coupon.
The valuation and risk analysis above is valid whatever the rate Ri is selected. It can be some last reset ``in-advance'' composition, last recent or even a random number. For operational purposes, it is enough that it is selected at the start of the period and for valuation/risk purposes, it is enough that it is consider as an advance on interest due with the difference embedded in the notional and not a final interest amount.
Advantages
In a recent consultation paper from the ECB, the feature of this approach has been incorrectly described as creating significant operational complexity, with more complex and less transparent calculation and relevant hedging issues expected. Based on the description provided above, it is clear that those element are inaccurate. As the paper does not provide any reference to relevant literature or explanation about the reason of those characteristics, we believe that further analysis of those issues are warranted.
One of the issues with compounded in-arrears mechanisms is that the payment has to take place on the same day that the final amount is known. This mechanism is not different from other in-arrears in that respect. In this context, the obvious advantage of the hybrid approach is that the issue appears only once, on the very last payment. The same range of solution discussed for the in-arrears can be used in this case also. This is a different discussion that is not debated here. Without doubt, the issues is easier in this case as it is relevant only on the last payment instead at each payment.
Operational ease/cash flow management
As mentioned above the operational ease and cash flow management issues are better in this mechanism. All cash flows, except the last are know at the period start.
Computational ease/mechanics
The only small issues is the new notional computation. Computing the coupon for in-arrears on a 3 month coupon (60 business days) take approximately 120 multiplications and 60 additions. The notional computation in the hybrid case requires one extra multiplication and one extra addition. If the usual (credit/profit) spread is added to the picture, as the rate fixed in advance plays the same theoretical role as the spread, the extra complexity is only one addition.
Hedging ease
In term of hedging, the notion of hedging ease or complexity is obviously relative to what is the target risk. Here we suppose that the target is to have not market risk and that the composition of overnight rates is considered risk free. In that case, most of the risk is on the composition and does not need any hedging. The only difference is that the notional is slightly changing at each period. The rate fixed at each period does not need any hedging, it is used as a repayment of part of the notional at each step. The addition of a spread may require a hedging in the same way as the addition of a spread may require a hedging with pure in-arrears coupons.
The credit risk of such a bond is not significantly different to the one of other bonds. No specific changes are required.
Usage and client acceptance
This type of bond/loan is not used currently. The acceptance by clients is unknown. The consultation paper mentioned above indicates that such mechanism are not observed. It indicates, without explanation, that the client acceptance is potentially low. As long as the adverb potentially is used, this is true. It would as true to say that the client acceptance is potentially very high.
Advances on final bills are a standard concept in retail and services. There is no reason that such a simple and widely used concept would not be accepted by sophisticated participants in the financial markets.
Next step
We have contacted the ECB/Working group to require a correction of the consultation paper.
A preprint version of this text will be made available on a preprint server soon. The link will be added.
Note added 2021-01-02: We have not yet received any answer from the ECB/Working group.
The new working paper related to the principal adjustment method for bonds and loans as been made available on SSRN:
The paper is available on SSRN at