Swap Rates and Term Structure Modelling: Implementation

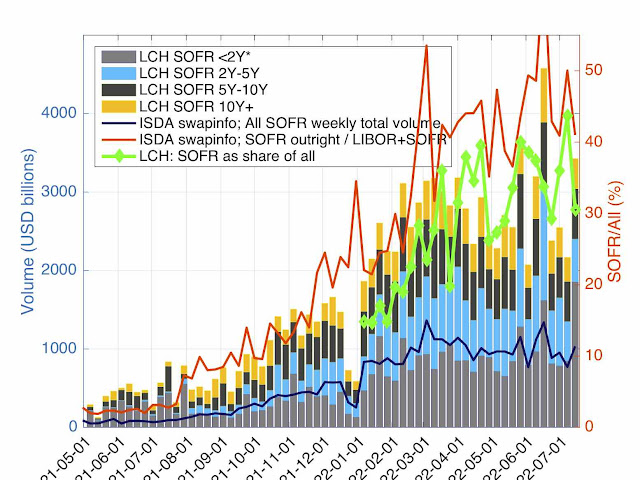
Swap rate dependent products, e.g. CMS, have a long history in interest rate modelling. They look simple as only one rate is involved, but when the rate is not paid in a natural way, i.e. not according to its own annuity, they involve some type of "convexity" or "timing" adjustment.

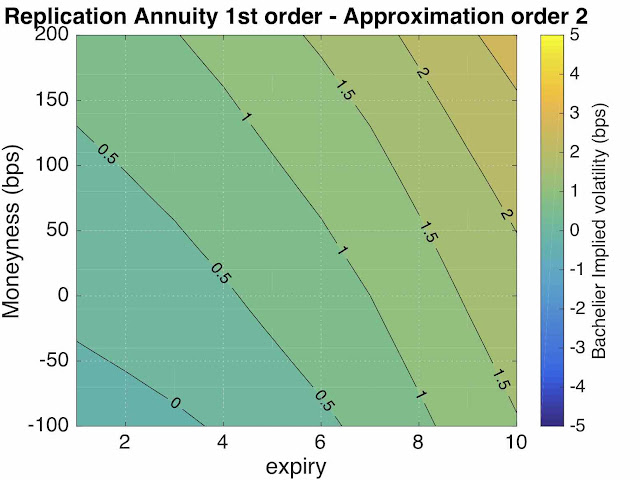
Those products are often priced using "replication", but to do so, some approximation of the annuity discounting, or absence thereof, is used. This type of single factor approximation is what we used in our recent paper on pricing cash settled swaption through the fallback published this month in Risk (Henrard (2022)).

A very recent paper Bang and Daboussi (2022) is proposing a new approach to price swap rate dependent products in a way that preserves the full marginal distribution of all the swaps and a user selected copula between those rates.

The implementation is not trivial from a quantitative finance perspective (two changes of measure) and implementation (Monte Carlo). But by the way the numerical approach is cleverly designed, the simulations are not too costly and converge quickly.

We have adapted the methodology proposed by the authors to take into account conventions (accrual factors not all the same and the T+2 payment/effective date) and implemented it in our library. This is the library we use for consulting and model validation purposes.

The results we have observed are very good. In their paper, the authors compare the (input) market smile to the (output) model generated smile for vanilla options and find a very small discrepancy, i.e. the numerical noise is small on the present value. We have obtained the same results. We have also done the comparison for the smile risk which was not presented in the paper. We computed the sensitivities to the alpha, beta, rho and nu parameters in a SABR model. In our implementation, the sensitivities are obtained by Algorithmic Differentiation (AD) as you would expect. For a 2Yx5Y swaption, here is the comparison between the analytic result (direct formula for the vanilla) and the Monte Carlo with AD version:

As you can see, the numerical noise is below 0.05% of the actual number on the alpha-vega (a little bit higher for nu and rho). This was obtained with a relatively low number of Monte Carlo paths (1,000).

Why we are interested by this approach, beyond its natural application to CMS, is for the above mentioned fallback of cash settled swaptions with the LIBOR-linked swap rate discontinuation.

With a precise view of the term structure smile risk in CMS-like products, we can now have a look at term structure smile risk for the fallback. That will be the subject of a forthcoming blog.

---

Henrard, M. (2022). Swap rate: cash settled swaptions in the fallback. Risk, Cutting Edge. Published online 1 July 2022. https://www.risk.net/cutting-edge/banking/7951001/swap-rate-cash-settled-swaptions-in-the-fallback

Bang, D. and Daboussi, E. (2022). Modelling of CMS-linked products in an RFR framework, with extension to hybrids, forward starting and canary options. SSRN 4134438. https://ssrn.com/abstract=4134438

---

Don't hesitate to contact us if you are interested by model developments or model validation related to swap rate linked products like CMS.

---

Added 2023-05-07: The implementation notes for this model have now been published in the muRis_Q Advisory Implementation Notes series. See the new related post.

LIBOR Transition: Back to "LIBOR First" - again!

Same title as 3 weeks ago!

LIBOR is again the first benchmark in USD this week at LCH!

Figure 1: Weekly share by product types at LCH

LIBOR, EFFR and SOFR still playing yo-yo!

USD-LIBOR trading should have stopped more than 6 month ago, but in the market figures there is still large activity around it. From week to week, the dominant benchmark in the USD derivative market change from LIBOR to SOFR to EFFR. Last week the winner was EFFR, the week before it was SOFR and another week before is was LIBOR.

Figure 1: Weekly share by product types at LCH

We are still far away from a all-in in SOFR; maybe we will never go there!

Figure 2: Weekly SOFR volume at LCH and as reported by ISDA (US regulatory figures based).

Getting closer to SOFR First!

Getting closer to SOFR First! The SOFR share at LCH was last week at 43.7%, highest share and getting closer to 50%.

Figure 1: Weekly share by product types at LCH

---

Note that there is no more LIBOR swaps outstanding at LCH in GBP and JPY. We had to wait July to make such an announcement as the last LIBOR-6M, fixed at the end of December, were paid at the end of June (GBP, T+0) and beginning of July (JPY, T+2). In CHF, there is still CHF 30 millions of LIBOR swaps outstanding; this is probably a LIBOR-12M swap with one coupon still to be paid.

LIBOR Transition: Back to "LIBOR First"

For the first time in a while, we are back to "LIBOR First" at LCH and for US regulatory figures.

Figure 1: Weekly share by product types at LCH

The story told by the ISDA published US regulatory figures is similar (see Figure 2). For those figures also, LIBOR is back to the fore. This can be seen with the ratio SOFR outright/(LIBOR+SOFR) which is back below 50%.

Figure 2: Weekly SOFR volume at LCH and as reported by ISDA (US regulatory figures based).

There are more and more discussion about allowing a wider use of the SOFR Term rate. This is based on its usage in cash products. Derivatives are (or at least should be) designed to help risk management. If derivatives cannot be based on the same underlying benchmark as the cash product, they become less useful. This is the case for Term Rate based swaps but also optional products like cap/floor. Some cash products have explicit or implicit cap or floor, but currently they cannot be hedged easily in the wholesale market.

Issues regarding the SOFR Term rate itself can also been seen in Figure 2. The short term part of the SOFR-OIS (less than 2 year) is not large. This means that it is difficult to established a term rate based on liquid regulated electronic trading venues (Level 1 waterfall). We have mentioned this issue in several blogs and presentation (see here for example). Currently, CME SOFR Term rate is based on level 3 of the waterfall (futures) and IBA SOFR Term rate is based on level 2 of the waterfall (dealer to client). Also when using futures, creating the term rate requires some arbitrary interpolation scheme choice and has some timing issue.

With only one year to go to the LIBOR end date, this is not very good for the transition!

Published paper: Swap Rate: cash settled swaptions in the fallback

The paper on the swap rate fallback and its impact on cash-settled swaptions announced in March has now been published in Risk.

Swap Rate: cash settled swaptions in the fallback

The paper is available on the Risk web site at

www.risk.net/7951001.

Abstract

With the planned cessation of LIBOR, the LIBOR-based Swap Rates will also cease. For legacy transactions linked to it, a fallback is required. Some approximated fallback mechanisms have been proposed by working groups. The approximations involve some non-linear function of overnight-based swap rates. Due to the non-linearity, cash settled vanilla swaptions are becoming exotic products. Moreover, keeping the annuity unchanged while changing the rate to overnight-based swap generates technical issues in the pricing leading to convexity adjustments. The article proposes different pricing methodologies for those now exotic swaptions, including several price approximation to reduce the implementation numerical complexity.

One graph from the paper: Error between replication with annuity ratio and order 2 approximation.