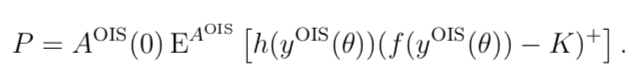Swap Rate: cash settled swaptions in the fallback
Different working groups have proposed fallbacks for the Swap Rates indirectly based on the mechanism used for LIBOR itself. This is the case of the Sterling working group in Working Group on Sterling Risk-Free Reference Rates and the USD working group in ARRC (2021). Those fallbacks are based on OIS versions of the Swap Rates. IBA is publishing GBP SONIA ICE Swap Rate since 14 December 2020 and USD SOFR Swap rate since 8 November 2021. Refinitiv is publishing the Tona Tokyo Swap Rate since 28 October 2021.
For reasons summarised below, it is not possible to create a Swap Rate's fallback coherent with the LIBOR's fallback. Or more precisely it is possible (and easy) for a quant to do so, based on the swap market globally, but it is impossible for a lawyer in a definition involving a single number. The self-imposed restriction on the fallback type available make the existence of a coherent fallback impossible. In the absence of an exactly coherent fallback, the above mentioned working groups' documents tried to provide formulas for an approximatively coherent one.
In this paper we do not discuss the quality of the approximation — some discussions are available in one of Marc's blogs — but the impact of the type of fallback selected on a liquid vanilla market instrument: cash settled swaptions with collateral discounting.
The proposed replacement for GBP LIBOR ISR by the Working Group on Sterling Risk-Free Reference Rates (2021) is displayed in Figure 1. Formulas with similar mechanisms have been proposed for USD and JPY.
Figure 1. Approximated formula proposed by the WGSRFRR for ICE Swap Rate fallback.
After fallback, a cash settled swaptions with collateral discounting payoff becomes
The non-linear pay-off part of the problem will be decomposed in two issues: strike and exotic feature. As the rate is transformed by a non-linear function, finding at which OIS rate the former IRS swaption will be exercised requires a little bit of work: inverting the function f. Once the strike is known, there is the question of the payoff, which is given by the same non-linear function. It is not a vanilla swaption anymore; a simple strike's shift or multiplier is not enough. In our pricing approach we provide approximations that estimate the impacts of the different parts.
The swaption value is usually obtained by expectation in the IRS physical annuity associated measure. The two issues are the ``wrong'' annuity and the non-linearity f.
We first change the measure to the OIS physical annuity associated measure. Then we approximate the ratio of annuities by a function h of the OIS rate:
Using standard replication argument, the price can then be written as
The paper also proposes several approximation to the price by full replication. The approximations are based on simple change of strike, order 1 approximation and order 2- approximation. The approximation can be used for themselves in case of short term options. We use them mainly to clarify which issues have a significant impact on the price.
The replication formulas and all the approximations have been implemented in our production grade library.
Preliminary versions of the results were presented at The 4th Interest Rate Reform Conference (20-21 October 2021) and at The 17th Quantitative Finance Conference (17-19 November 2021).
The full paper has been submitted for publication in November.
Don't hesitate to contact us if you want to implement such approach or validate your own implementation.